Capítulo 2 Conceptos Introductorios
2.1 Teoría de conjuntos
Definición2.1 Un conjunto es una colección bien definida de objetos, llamados sus elementos. Los conjuntos se simbolizan con letras mayúsculas \(A\), \(B\), \(...\) Los objetos que componen el conjunto se denominan elementos y se denotan con letras minúsculas \(a, b, ...\) [Tomado de (zill2012algebra?) pág \(21\)]
Definición2.2 Para definir un conjunto por extensión, se enumeran todos sus elementos separándolos por comas y luego se encierran entre llaves.
Para escribir un conjunto por comprensión se elige un elemento arbitrario \(x\) y se señala que cumple la propiedad \(P(x)\). Finalmente, se encierra toda la expresión entre llaves. [Tomado de (zill2012algebra?) pág \(22\)]
\[ A=\{ x | x \ \ \text{cumple la propiedad} \ \ P(x) \} \]
Definición2.3 Diremos que dos conjutnos \(A\) y \(B\) son iguales si tienen los mismos elementos. Para indicar que \(A\) y \(B\) son iguales se escribe:[Tomado de (zill2012algebra?) pág \(22\)]
\[ A=B \]
Nota:. Un conjunto que posee un número finito de elementos; se llaman conjuntos finitos.
Un conjunto que no tiene un número finito de elemenos se llaman conjunto infinito.
[Tomado de (zill2012algebra?) pág \(23\)]
Definición2.4 El número de elementos de un conjunto finito es lo que se llama la cardinalidad de dicho conjunto. La cardinalidad de un conjunto finito \(A\) se denota por: [Tomado de (zill2012algebra?) pág \(24\)]
\[ Card(A) \ \ \ \text{ó} \ \ \ |A| \]
Definición2.5 Dos conjuntos finitos \(X\) y \(Y\) se dicen ser equipotentes si tienen exactamente el mismo número de elementos. [Tomado de (zill2012algebra?) pág \(24\)]
Definición2.6 Un conjunto se dice vacío si no posee elementos. El conjunto vacío se denota como:
\[ \{ \} \ \ \ \text{ó} \ \ \ \Phi \]
Definición2.7 El conjunto universal se define como el conjunto que posee todos los elementos de todos los conjunots, y se denota como:[Tomado de (zill2012algebra?) pág \(25\)]
\[ \text{Conjunto universal:} \ \ \ U \]
Definición2.8 Si cada elemento de un conjunto \(A\) es también elemento de un conjunto \(B\), entonces se dice que \(A\) es un subconjunto de \(B\). Se dice también que \(A\) está contenido en \(B\) o que \(B\) contiene a \(A\). La relación de subconjunto se denota como: [Tomado de (zill2012algebra?) pág \(25\)]
\[ A \subset B \ \ \ \text{ó} \ \ \ B \supset A \]
\[ A \subset B \ \ \ \text{si y sólo si } \ \ \ \ \text{Para todo } x, \ \ \ \ \ x \in A \ \ \ \text{entonces } \ \ \ x \in B \]
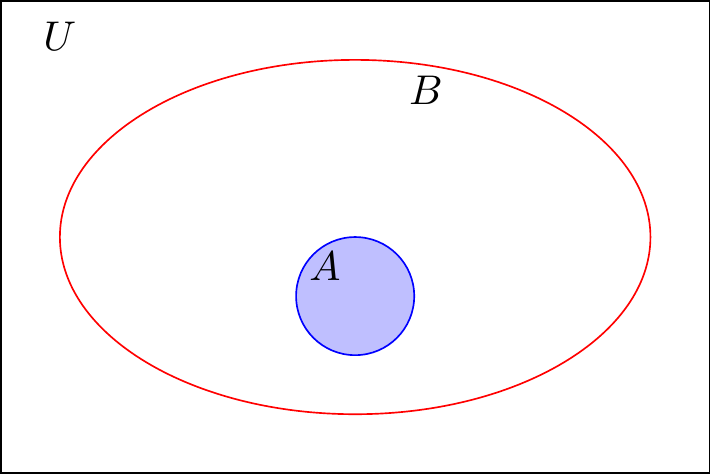
Figura 2.1: Inclusión de conjuntos
Definición2.9 La unión de dos conjuntos \(A\) y \(B\) consta de todos los elementos que pertenecen a \(A\) o a \(B\). La unión de \(A\) y \(B\) se denota por \(A \cup B\). [Tomado de (zill2012algebra?) pág \(31\)]
\[ A \cup B = \{ x | x \in A \ \text{o} \ x \in B\} \]
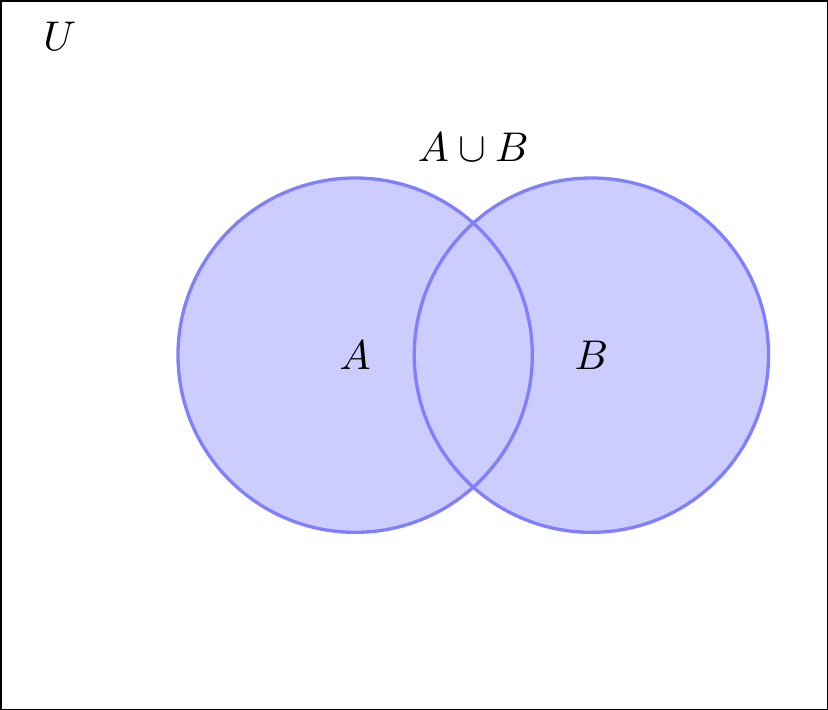
Figura 2.2: Unión de conjuntos
2.2 Propiedades de la Unión
\[ \begin{matrix} (a) & A \cup B = B \cup A & \text{propiedad conmutativa} \\ (b) & (A \cup B) \cup C = A \cup (B \cup C) & \text{propiedad asociativa} \\ (c) & A \cup \Phi = A & \text{propiedad de la existencia para la identidad} \\ (d) & A \cup U = U & \text{propiedad de la existencia del conjunto absorbente} \end{matrix} \]
Definición2.10 La intersección de dos conjuntos \(A\) y \(B\) consta de todos los elementos que pertenecen a \(A\) y a \(B\). La intersección de \(A\) y \(B\) se denota por \(A \cap B\). [Tomado de (zill2012algebra?) pág \(30\)]
\[ A \cap B = \{ x | x \in A \ \text{y} \ x \in B\} \]
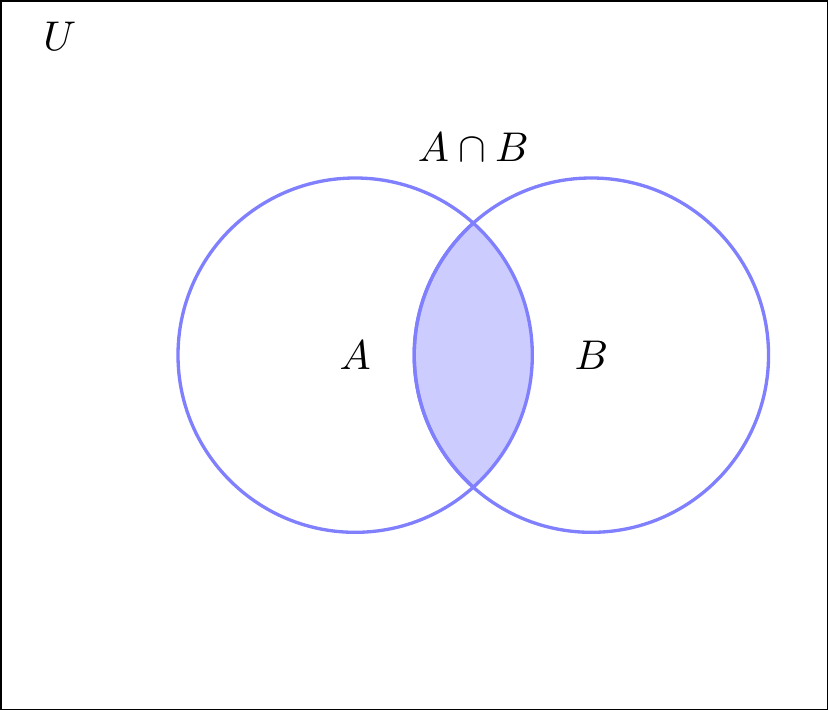
Figura 2.3: Intersección de conjuntos
2.3 Propiedades de la Intersección
\[ \begin{matrix} (a) & A \cap B = B \cap A & \text{propiedad conmutativa} \\ (b) & (A \cap B) \cap C = A \cap (B \cap C) & \text{propiedad asociativa} \\ (c) & A \cap U = A & \text{propiedad de la existencia para la identidad} \\ (d) & A \cap \Phi = \Phi & \text{propiedad de la existencia del conjunto absorbente} \end{matrix} \]
2.4 Propiedades de la unión y la intersección
\[ \begin{matrix} (a) & A \cup (B \cap C) = (A \cup B) \cap (A \cup C) & \text{prop dist de la unión respecto a la intersección} \\ (b) & A \cap (B \cup C) = (A \cap B) \cup (A \cap C) & \text{prop dist de la intersección respecto a la unión} \end{matrix} \]
2.5 Diferencia entre dos conjuntos
Definición2.11 La diferencia de dos conjuntos \(A\) y \(B\) consta de todos los elementos que pertenecen a \(A\) y no pertenecen a \(B\). La diferencia de \(A\) y \(B\) se denota por \(A - B\). [Tomado de (zill2012algebra?) pág \(34\)]
\[ A - B = \{ x | x \in A \ \text{y} \ x \notin B\} \]
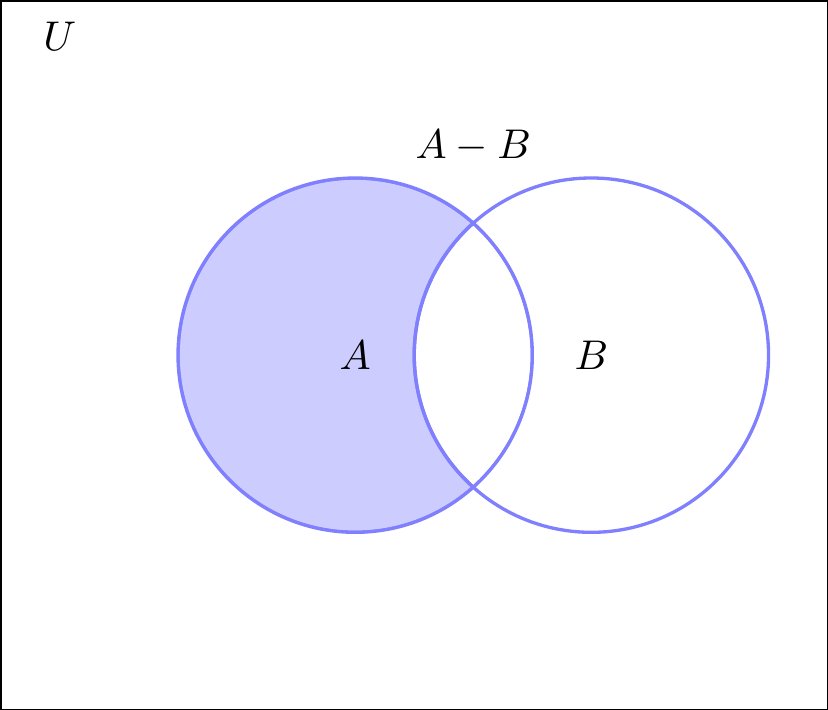
Figura 2.4: Diferencia de conjuntos
\[ B - A = \{ x | x \in B \ \text{y} \ x \notin A\} \]
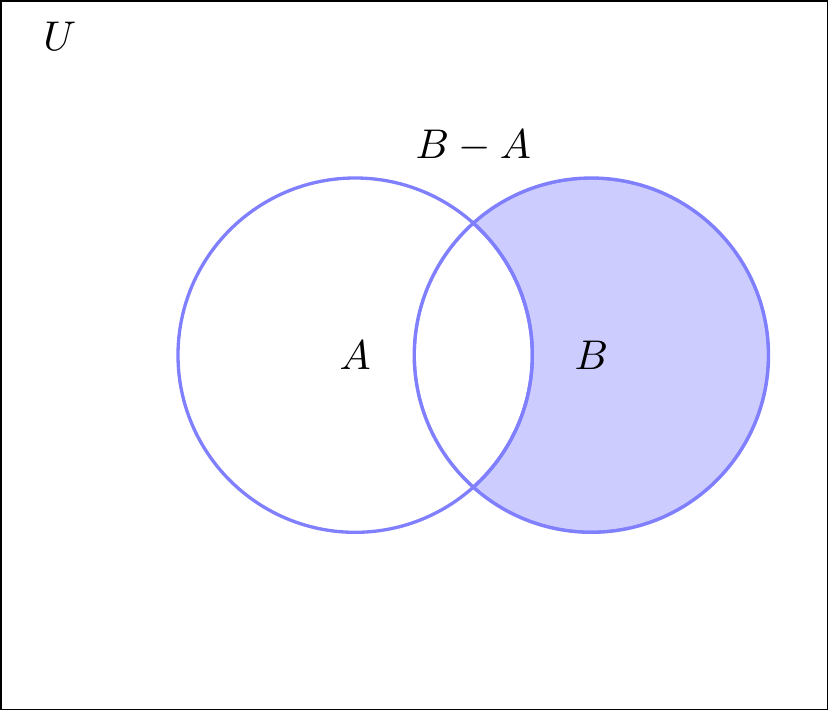
Figura 2.5: Diferencia de conjuntos
2.6 Complemento de un conjunto
Definición2.12 El complemento de un conjunto \(A\) consta de todos los elementos del universo \(U\), y que no pertenecen a \(A\). El complemento de \(A\) se denota por \(A^{c}\). [Tomado de (zill2012algebra?) pág \(34\)]
\[ A'=A^{c} = \{ x | x \notin A \} \]
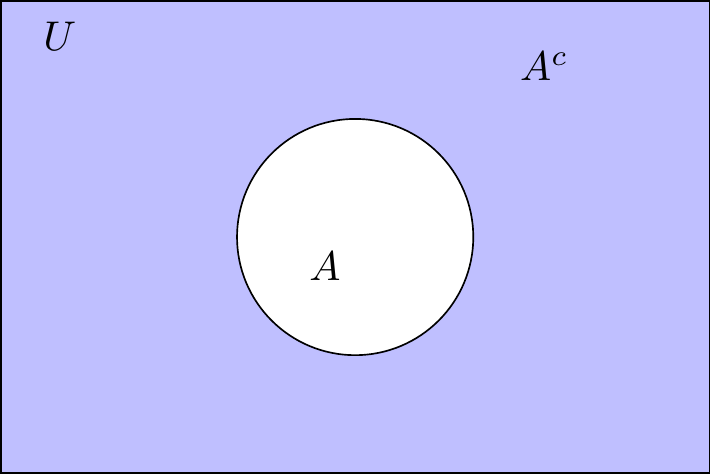
Figura 2.6: Complemento de un conjunto
2.7 Diferencia simétrica de dos conjuntos
Definición2.13 La diferencia simétrica entre dos conjuntos \(A\) y \(B\) se define como el conjunto de todos los elementos del universo \(U\), que pertenecen a \((A-B) \cup (B-A)\).

Figura 2.7: Diferencia simétrica de conjuntos
2.8 Propiedades del algebra de conjuntos
\[\begin{equation} \begin{matrix} \text{Leyes de idemponentes} & &\\ (1a) \ \ A \cup A = A & (1b) \ \ A \cap A = A &\\ & & &\\ \text{Leyes asociativas} & &\\ (2a) \ \ (A \cup B) \cup C = A \cup (B \cup C) & (2b) \ \ (A \cap B) \cap C = A \cap (B \cap C) &\\ & & &\\ \text{Leyes conmutativas} & &\\ (3a) \ \ A \cup B = B \cup A & (3b) \ \ A \cap B = B \cap A &\\ & & &\\ \text{Leyes distributivas} & &\\ (4a) \ \ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) & (4b) \ \ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) &\\ & & &\\ \text{Leyes de identidad y absorción} & &\\ (5a) \ \ A \cup \Phi = A & (5b) \ \ A \cap U = A &\\ (6a) \ \ A \cup U = U & (6b) \ \ A \cap \Phi = \Phi &\\ & & &\\ \text{Ley involutiva} & &\\ (7a) \ \ (A^{c})^{c}=A & &\\ & & &\\ \text{Leyes del complementario} & &\\ (8a) \ \ A \cup A^{c} = U & (8b) \ \ A \cap A^{c} = \Phi &\\ (9a) \ \ U^{c} = \Phi & (9b) \ \ {\Phi}^{c} = U \\ & & &\\ \text{Leyes de De Morgan} & &\\ (10a) \ \ (A \cup B)^{c} = A^{c} \cap B^{c} & (10b) \ \ (A \cap B)^{c} = A^{c}\cup B^{c} \end{matrix} \end{equation}\]
2.9 Operaciones con conjuntos
Esta es una aplicación que muestra graficamente las operaciones entre tres conjuntos, el Autor:LikitMaths (https://www.geogebra.org/m/QWS4wDtE) las elaboro usando geogebra.
2.10 Ejemplo1
![Ejemplo 1 de conjuntos [Imagen tomada de [@zill2012algebra] pág $33$]](images/EjemploConjuntos1.jpg)
Figura 2.8: Ejemplo 1 de conjuntos [Imagen tomada de (zill2012algebra?) pág \(33\)]
A partir de la figura 2.8, obtener la solución a los enunciados de conjuntos
Obtener \(A \cup B=?\)
Obtener \(A \cup C=?\)
Obtener \(C \cup B=?\)
Obtener \(A \cap B=?\)
Obtener \(A \cap C=?\)
Obtener \(C \cap B=?\)
Obtener \(A - B=?\)
Obtener \(B - A=?\)
Obtener \(A - C=?\)
Obtener \(C - B=?\)
Obtener \(B - C=?\)
Obtener \((A\cap B) - C=?\)
Obtener \((C\cap B) - A=?\)
2.11 Ejemplo2
![Ejemplo 2 de conjuntos [Imagen tomada de [@zill2012algebra] pág $35$]](images/EjemploConjuntos2.jpg)
Figura 2.9: Ejemplo 2 de conjuntos [Imagen tomada de (zill2012algebra?) pág \(35\)]
A partir de la figura 2.9, obtener la solución a los enunciados de conjuntos
Obtener \(A \cup B=?\)
Obtener \(A \cap B=?\)
Obtener \(A - B=?\)
Obtener \(B - A=?\)
2.12 Ejemplo3
![Ejemplo 3 de conjuntos [Imagen tomada de [@zill2012algebra] pág $33$]](images/EjemploConjuntos3.jpg)
Figura 2.10: Ejemplo 3 de conjuntos [Imagen tomada de (zill2012algebra?) pág \(33\)]
A partir de la figura 2.10, obtener la solución a los enunciados de conjuntos
Obtener \({\bigcup}_{i=1}^{2}A_{i} =?\)
Obtener \({\bigcap}_{i=2}^{3}A_{i} =?\)
Obtener \({\bigcup}_{i=1}^{3}A_{i} =?\)
Obtener \({\bigcap}_{i=1}^{2}A_{i} =?\)
Obtener \({\bigcap}_{i=2}^{3}A'_{i} =?\)
Obtener \({\bigcap}_{i=1}^{3}A_{i} =?\)
Obtener \(\left({\bigcup}_{i=1}^{2}A_{i}\right) - A_3=?\)
Obtener \(A_1-\left({\bigcup}_{i=2}^{3}A_{i}\right)=?\)
2.13 Ejemplos de cardinalidad
Suponer que para cada uno de los siguientes ejmplos el cardinal del universo (e.d \(U\) ) es la suma de las magnitudes que representan los números en la gráfica.
2.13.1 Primer ejemplo dos conjuntos
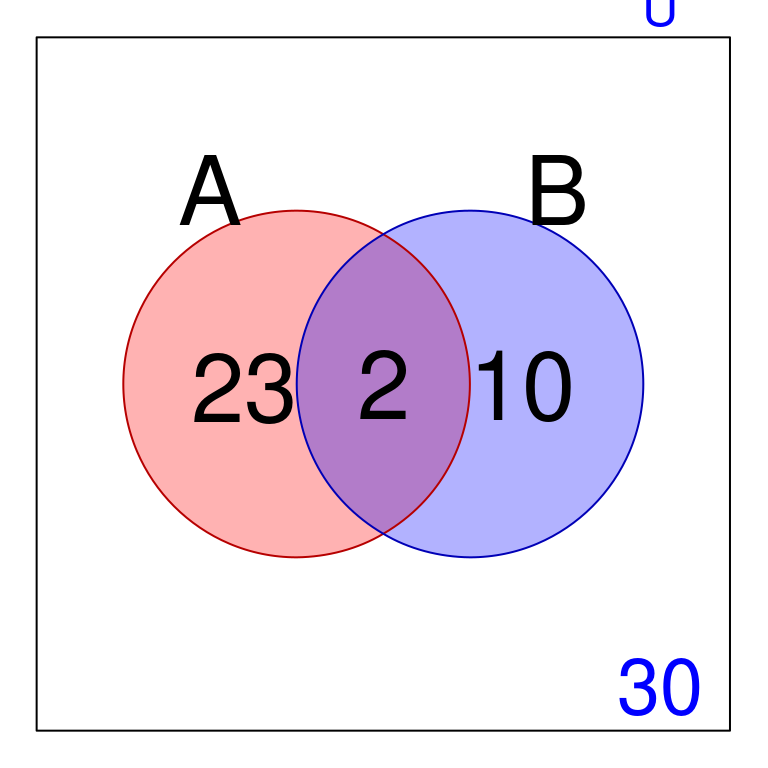
A partir de la gáfica, obtener la solución a los enunciados de conjuntos:
Obtener el cardinal de \(A \cup B=?\)
Obtener el cardinal de \(A \cap B=?\)
Obtener el cardinal de \(A - B=?\)
Obtener el cardinal de \(B - A=?\)
Obtener el cardinal para el complemento de \(B - A=?\)
2.13.2 Segundo ejemplo tres conjuntos
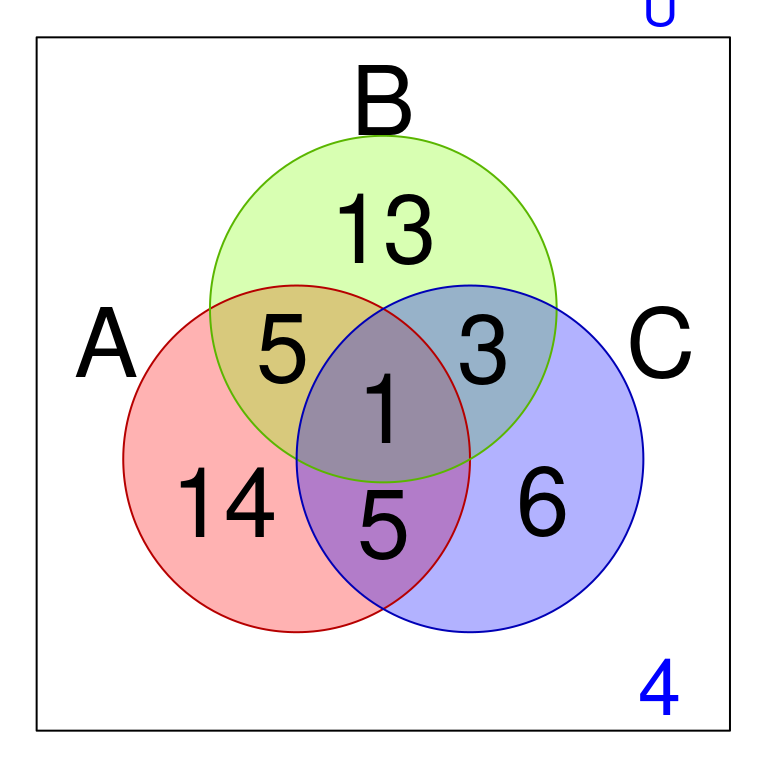
A partir de la gáfica, obtener la solución a los enunciados de conjuntos:
Obtener el cardinal de \(A=?\)
Obtener el cardinal de \(B=?\)
Obtener el cardinal de \(C=?\)
Obtener el cardinal de \((A - B) \cup (B-A)=?\)
Obtener el cardinal de \((C - B) \cup (B-C)=?\)
Obtener el cardinal de \(B \cap A \cap C=?\)
Obtener el cardinal para el complemento de \(B - A=?\)
Obtener el cardinal de \(A \cup B=?\)
Obtener el cardinal de \(A \cap B=?\)
Obtener el cardinal de \(A - B=?\)
Obtener el cardinal de \(B - A=?\)
Obtener el cardinal para el complemento de \(C - A=?\)
2.13.3 Tercer ejemplo cuatro conjuntos

A partir de la gáfica, obtener la solución a los enunciados de conjuntos:
Obtener el cardinal de \(A=?\)
Obtener el cardinal de \(B=?\)
Obtener el cardinal de \(C=?\)
Obtener el cardinal de \(D=?\)
Obtener el cardinal de \((A - B) \cup (B-A)=?\)
Obtener el cardinal de \((C - B) \cup (B-C)=?\)
Obtener el cardinal de \((C - D) \cup (D-C)=?\)
Obtener el cardinal de \(D \cap A \cap C=?\)
Obtener el cardinal para el complemento de \(C - A=?\)
Obtener el cardinal de \(A \cup D=?\)
Obtener el cardinal de \(D \cap B=?\)
Obtener el cardinal de \(A - B=?\)
Obtener el cardinal de \(C - A=?\)
Obtener el cardinal para el complemento de \(D - A=?\)
2.13.4 Cuarto ejemplo (lectura de revistas)
En un grupo universal (\(U\)) para lectura se tienen tres subgrupos de lectura para las revistas \(A\), \(B\), y \(C\).
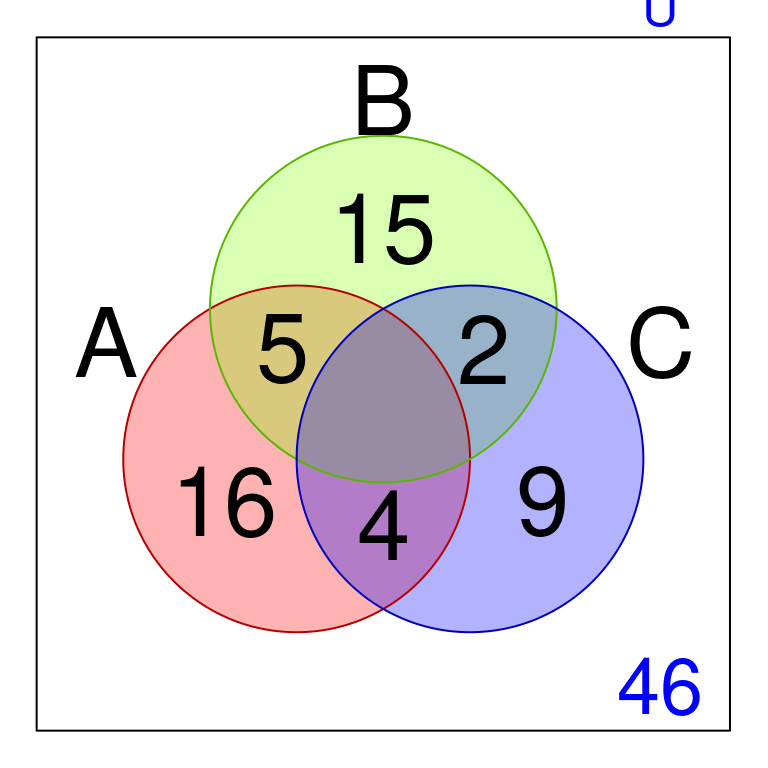
A partir de la gáfica, obtener la solución a los enunciados de conjuntos:
Obtener el cardinal de lectura para la revista \(A=?\)
Obtener el cardinal de lectura para la revista \(B=?\)
Obtener el cardinal de lectura para la revista \(C=?\)
Qué significa el cardinal de \((A - B) \cup (B-A)\) para el grupo de lectura?.
Qué significa el cardinal de \((C - B) \cup (B-C)\) para el grupo de lectura?.
Qué significa el cardinal de \(B \cap A \cap C\) para el grupo de lectura?.
Qué significa el cardinal del complemento \(B - A\) para el grupo de lectura?.
Cúal es el cardinal de los que no leen las tres revistas?